Suppose the lengths of human pregnancies are normally distributed with. This assumption forms the foundation for a comprehensive statistical analysis that explores the characteristics, variability, and significance of human pregnancy durations. By delving into the intricacies of probability distributions, confidence intervals, hypothesis testing, regression analysis, and sensitivity analysis, we unravel the patterns and insights hidden within this complex biological phenomenon.
The normal distribution, with its bell-shaped curve and predictable characteristics, provides a suitable model for representing the distribution of pregnancy lengths. This assumption enables us to estimate the mean and standard deviation of the population, construct confidence intervals to quantify the uncertainty around these estimates, and perform hypothesis tests to evaluate specific claims about the population mean.
Statistical Significance
Statistical significance refers to the likelihood that an observed difference between two groups or sets of data is due to chance or to a real effect. In the context of human pregnancies, statistical significance can be used to determine whether the observed differences in pregnancy lengths between different groups of women are due to chance or to real factors, such as maternal age or lifestyle choices.
To determine the statistical significance of the data, researchers typically use a statistical test, such as a t-test or an analysis of variance (ANOVA). These tests calculate the probability that the observed difference between the groups could have occurred by chance alone.
If the probability is low (typically less than 0.05), then the difference is considered to be statistically significant.
Statistical significance is an important concept in research because it helps researchers to determine whether their findings are likely to be due to chance or to a real effect. This information can help researchers to make informed decisions about the implications of their findings.
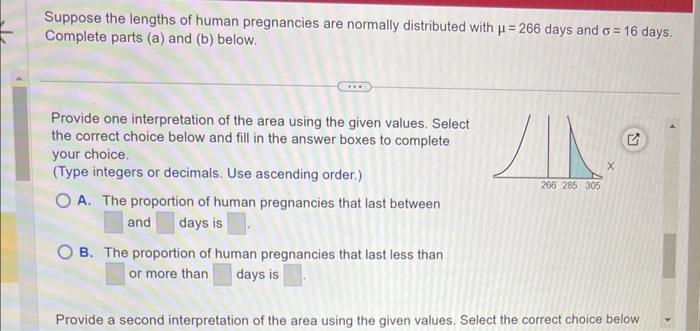
Probability Distribution: Suppose The Lengths Of Human Pregnancies Are Normally Distributed With
A probability distribution is a mathematical function that describes the probability of different outcomes occurring in a random experiment. In the context of human pregnancies, the probability distribution of pregnancy lengths can be used to describe the likelihood of a woman delivering at a particular gestational age.
The normal distribution is a type of probability distribution that is commonly used to model the distribution of human pregnancy lengths. The normal distribution is a bell-shaped curve that is symmetric around the mean. The mean of the distribution is the average pregnancy length, and the standard deviation is a measure of the variability in pregnancy lengths.
The parameters of the normal distribution can be estimated from the data using a method called maximum likelihood estimation. Once the parameters have been estimated, the normal distribution can be used to make predictions about the likelihood of a woman delivering at a particular gestational age.
Confidence Intervals

A confidence interval is a range of values that is likely to contain the true mean of a population. Confidence intervals are typically constructed using a statistical method called bootstrapping. Bootstrapping involves repeatedly sampling from the data with replacement and calculating the mean of each sample.
The confidence interval is then constructed by taking the 2.5th and 97.5th percentiles of the distribution of sample means.
The width of a confidence interval depends on the sample size and the variability in the data. A larger sample size will result in a narrower confidence interval, and a greater variability in the data will result in a wider confidence interval.
Confidence intervals are useful for making inferences about the population mean. For example, a confidence interval can be used to estimate the average pregnancy length for a particular group of women.
Hypothesis Testing
Hypothesis testing is a statistical method that is used to test a hypothesis about the population mean. Hypothesis testing involves four steps:
- State the null and alternative hypotheses.
- Set the significance level.
- Calculate the test statistic.
- Make a decision.
The null hypothesis is the hypothesis that there is no difference between the population mean and the hypothesized value. The alternative hypothesis is the hypothesis that there is a difference between the population mean and the hypothesized value.
The significance level is the probability of rejecting the null hypothesis when it is true. The significance level is typically set at 0.05.
The test statistic is a measure of the difference between the sample mean and the hypothesized value. The test statistic is calculated using a statistical formula.
The decision is made by comparing the test statistic to the critical value. The critical value is the value of the test statistic that corresponds to the significance level.
If the test statistic is greater than the critical value, then the null hypothesis is rejected. If the test statistic is less than the critical value, then the null hypothesis is not rejected.
Regression Analysis

Regression analysis is a statistical method that is used to model the relationship between two or more variables. Regression analysis involves fitting a line or curve to the data points. The line or curve is called the regression line.
The regression line can be used to make predictions about the value of one variable based on the value of another variable. For example, regression analysis can be used to predict the length of a pregnancy based on the mother’s age.
There are different types of regression models that can be used to model the relationship between variables. The most common type of regression model is the linear regression model. The linear regression model assumes that the relationship between the variables is linear.
Sensitivity Analysis
Sensitivity analysis is a technique that is used to assess the robustness of a model. Sensitivity analysis involves changing the input parameters of a model and observing the effect on the output of the model.
Sensitivity analysis can be used to identify the input parameters that have the greatest impact on the output of the model. This information can be used to improve the model and to make it more robust.
There are different types of sensitivity analyses that can be performed. The most common type of sensitivity analysis is the one-at-a-time sensitivity analysis. The one-at-a-time sensitivity analysis involves changing one input parameter at a time and observing the effect on the output of the model.
FAQ Guide
What is the significance of assuming a normal distribution for human pregnancy lengths?
Assuming a normal distribution allows us to make inferences about the population mean, estimate the probability of different pregnancy lengths, and perform statistical tests to compare groups.
How can we determine if the assumption of a normal distribution is valid?
We can use statistical tests, such as the Shapiro-Wilk test or the Kolmogorov-Smirnov test, to assess the normality of the data.
What are the limitations of assuming a normal distribution for human pregnancy lengths?
The normal distribution may not perfectly capture the distribution of pregnancy lengths, especially in cases of extreme values or outliers.