Delving into the realm of geometry, the Central Angles and Arc Measures Answer Key stands as an authoritative resource, providing a comprehensive understanding of these fundamental concepts. This guide unravels the intricate relationship between central angles and their corresponding arc measures, equipping readers with a profound knowledge that illuminates the intricacies of geometry.
Within this meticulously crafted guide, readers will embark on a journey through the measurement of central angles, unraveling the techniques employed to accurately quantify these angles. Furthermore, the formulas for calculating arc length and sector area are unveiled, empowering readers to delve into the geometric properties of sectors with precision.
Central Angles and Arc Measures: Central Angles And Arc Measures Answer Key
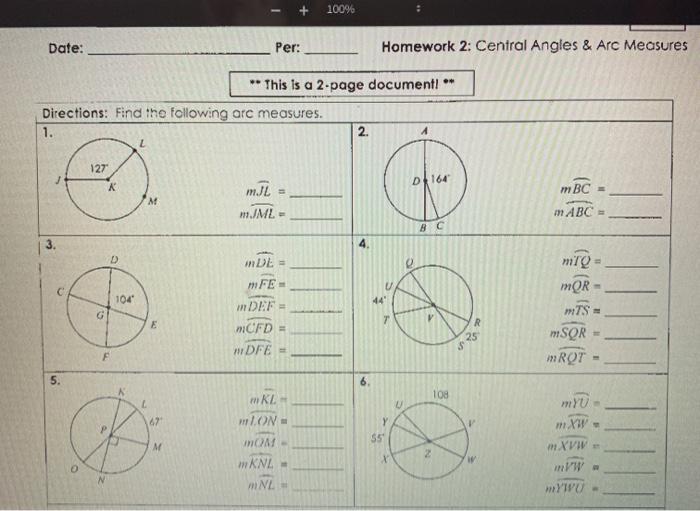
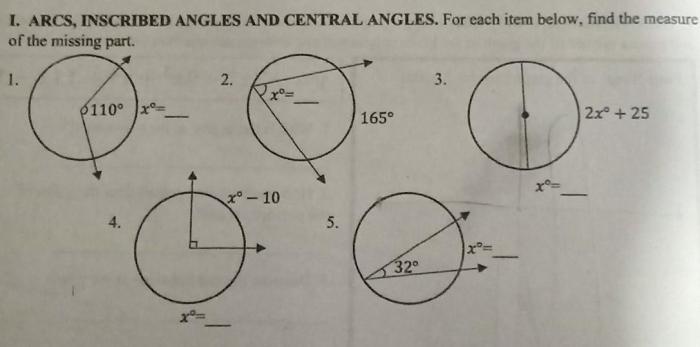
Central angles and arc measures are fundamental concepts in geometry, used to describe the angles and arcs associated with circles. These concepts play a crucial role in various mathematical applications and real-world scenarios.
Definition and Concepts
A central angle is an angle formed by two radii of a circle that share a common endpoint at the circle’s center. The measure of a central angle is equal to the fraction of the circle’s circumference that it intercepts.
Arc measures are used to describe the length of an arc, which is a portion of a circle’s circumference.
Inscribed angles are angles formed by two chords intersecting within a circle. The measure of an inscribed angle is half the measure of its intercepted central angle.
Measurement of Central Angles
Central angles can be measured using protractors or angle measures. Protractors are semicircular tools with degree markings, while angle measures are devices that can directly measure angles in degrees or radians.
Degrees and radians are two common units for measuring angles. One degree is equal to 1/360 of a full rotation, while one radian is equal to the angle formed by an arc length equal to the radius of the circle.
Arc Length and Area of Sectors, Central angles and arc measures answer key
The arc length of a sector is the length of the arc intercepted by the central angle. The formula for calculating the arc length is: arc length = (central angle measure / 360)- 2πr , where ris the radius of the circle.
The area of a sector is the area of the region enclosed by the arc and the two radii that form the central angle. The formula for calculating the area of a sector is: area = (central angle measure / 360)- πr² .
Applications and Examples
Central angles and arc measures have numerous applications in various fields:
- Navigation:Central angles are used to determine the direction and distance traveled in navigation systems.
- Astronomy:Central angles are used to measure the apparent size of celestial objects, such as the sun and moon.
- Engineering:Central angles are used in designing gears, pulleys, and other mechanical components.
- Architecture:Central angles are used in designing arches, domes, and other architectural structures.
Practice Problems and Solutions
| Problem | Solution |
|---|---|
| Find the measure of the central angle that intercepts an arc of length 10 cm on a circle with a radius of 5 cm. | (10 / 2π
|
| Calculate the area of a sector with a central angle of 60° and a radius of 10 cm. | (60 / 360)
|
FAQ Summary
What is the formula for calculating the arc length of a sector?
Arc length = (central angle/360) x 2πr
How do you convert degrees to radians?
Radians = Degrees x (π/180)
What is the relationship between the arc length, central angle, and radius of a sector?
Arc length is directly proportional to both the central angle and the radius of the sector.